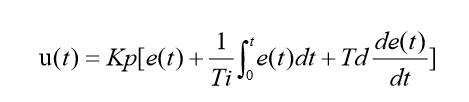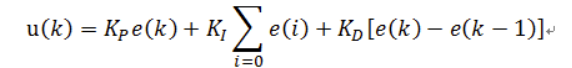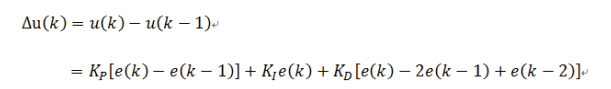PID基础

导言：

对于学习控制的同学来说，PID算法是我们非常常用的一种闭环反馈算法，我们常说的电机速度环，位置环，无人机的高度环，姿态环，都是利用嵌套的PID算法来实现的，但是明白原理很简单，上手还是比较难的，正好我们调试电机的任务中用到了PID算法，我们可以试一试手写一个PID算法，来让大家对PID有一个深刻的理解。
首先，我们要让一个系统趋于稳定，就要引入负反馈机制。打个简单的比方，如果闭着眼睛走路的话，就会撞墙，但是如果眼睛把墙的位置反馈给我们的话，我们就可以通过我们大脑来处理信息，绕过前面的墙
我们先理解一下负反馈是怎么帮我们实现自动控制的。还是上面那个例子，我们想向门走去，我们需要眼睛给我们反馈三个信息。
- 第一个是我们现在的距离和墙距离的差值，
- 第二个是我们在前几秒和墙位置的差值，因为根据两点一线原则，我们就可以通过历史位置来判断我们和墙的具体关系
- 最后一个信息就是我们向门走去的速度，这样就可以方便我们调节绕墙的速度。
我们把现在的位置信息反馈叫做P（比例），过去的位置信息累加叫做I（积分），速度也就是变化率信息叫做D（微分），这样我们就发现，这三个数据就是我们PID的三个字母。
以上PID公式就可以实现我们的闭环反馈，但是如何将我们的公式转换成代码呢？不同的代码表达决定了我们采用位置式PID还是增量式PID。

位置式PID：
首先我们先讲讲位置式PID。

e(k)是我们设定值和当前值的一个偏差，Σe(i）是我们开机开始偏差的一个求和，最后一个e(k)-e(k-1)就是近两次误差的差值

所以说我们只要把设定值和当前值的偏差输入到函数里，就可以得到我们的反馈值了，而反馈值的大小取决于我们PID的参数的调配，也就是Ki,Kp,Kd。

我们用代码可以这样实现

typedef struct {
    float P,I,D,limit
}PID;

typedef struct Error{
    float Current_Error;//当前误差
    float Last_Error;//上一次误差
    float Previous_Error;//上上次误差
}Error ;

float PID_Realize(Error *sptr,PID *pid,int32 NowPlace,float Point){
    int32 iError,//当前误差
    Realize;//实际输出

    iError=Point-NowPlace;//计算当前误差
    sptr->Current_Error+=pid->I*iError;//误差积分
    sptr->Current_Error=sptr->Current_Error>pid->limit?pid->limit:sptr->Current_Error;//积分限幅
    sptr->Current_Error=sptr->Current_Error<pid->limit?pid->limit:sptr->Current_Error;
    Realize=pid->P*iError//比例P
            +sptr->Current_Error//积分I
            +pid->D*(iError-sptr->Last_Error);//微分D
    sptr->Last_Error=iError;//更新上次误差
    return Realize;//返回实际值
}

以上代码给积分设一个上限，为什么呢？因为过去的误差是会一直增加的，如果情况不稳定的话，很有可能每次采样都为正，或者都为负，那么我们的求和值会一直叠加，加到最后变成无穷，只要Ki不是0，那么我们的代码将会跑飞，所以我们给它设一个阈值以防它跑飞，要是历史数据加到阈值时，就让他以阈值输出，告诉我们的系统，历史偏差已经达到了上限。

增量式PID：
我们再讲讲增量式PID。

增量式在位置式的基础上进行了又一次作差，也就是算了两次位置反馈量的差作为反馈量，在式子中间的积分项中，积分的Σ被除去了，留下的是一个单值，之前位置式那种设最大阈值的方法被取消，每次的修正值只与过去的三个参数有关，更加具有实时性。

typedef struct {
    float P,I,D,limit
}PID;

typedef struct Error{
    float Current_Error;//当前误差
    float Last_Error;//上一次误差
    float Previous_Error;//上上次误差
}Error ;

float PID_Increase(Error *sptr,PID *pid,int32 NowPlace,float Point){
    int32 iError,//当前误差
    Increase;//实际增量输出

    iError=Point-NowPlace;//计算当前误差
    Increase=pid->P*(iError- sptr->Last_Error)//比例P
            +pid->I*iError//积分I
            +pid->D*(iError-2*sptr->Last_Error+sptr->Previous_Error);//微分D
    sptr->Previous_Error=sptr->Last_Error;//更新前次误差
    sptr->Last_Error=iError;//更新上次误差
    return Increase;//返回增量
}

位置式PID优缺点：

优点：

①位置式PID是一种非递推式算法，可直接控制执行机构（如平衡小车），u(k)的值和执行机构的实际位置（如小车当前角度）是一一对应的，因此在执行机构不带积分部件的对象中可以很好应用

缺点：

①每次输出均与过去的状态有关，计算时要对e(k)进行累加，运算工作量大。

增量式PID优缺点：

优点：

①误动作时影响小，必要时可用逻辑判断的方法去掉出错数据。

②手动/自动切换时冲击小，便于实现无扰动切换。当计算机故障时，仍能保持原值。

③算式中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关。

缺点：

①积分截断效应大，有稳态误差；

②溢出的影响大。有的被控对象用增量式则不太好。

附录：

纯纯2022年电赛使用的pid的bsp

/**
  * @brief  init pid parameter
  * @param  pid struct
    @param  parameter
  * @retval None
  */
void pid_init(pid_struct_t *pid,
              float kp,
              float ki,
              float kd,
              float i_max,
              float out_max)
{
  pid->kp      = kp;
  pid->ki      = ki;
  pid->kd      = kd;
  pid->i_max   = i_max;
  pid->out_max = out_max;
}

/**
  * @brief  pid calculation
  * @param  pid struct
    @param  reference value
    @param  feedback value
  * @retval calculation result
  */
float pid_calc(pid_struct_t *pid, float ref, float fdb)
{
  pid->ref = ref;
  pid->fdb = fdb;
  pid->err[1] = pid->err[0];
  pid->err[0] = pid->ref - pid->fdb;

  pid->p_out  = pid->kp * pid->err[0];
  pid->i_out += pid->ki * pid->err[0];
  pid->d_out  = pid->kd * (pid->err[0] - pid->err[1]);
  if(pid->i_out > pid->i_max)
    {
        pid->i_out = pid->i_max;
    }
  pid->output = pid->p_out + pid->i_out + pid->d_out;

    if(pid->output > pid->out_max)
    {
        pid->output = pid->out_max;
    }
    else if(pid->output < -(pid->out_max))
    {
        pid->output = -(pid->out_max);
    }
  return pid->output;
}